IT未経験の私が
基本情報技術者試験の勉強をしていて、
つまずいたところや疑問に思った点を
アウトプットするシリーズです。
同じく基本情報技術者試験の勉強をしている方の参考になったら嬉しいです♪
試験合格を目指した覚え方・考え方かつ未経験独学なので、
実務的な理解方法とは異なる場合があります。
Contents
今回のテーマ:論理演算
今回は、論理演算について理解していきます。
範囲情報
・科目A:テクノロジ系
・基礎理論
よく出てくるのでしっかり理解しておくべき!
今回の用語
MIL記号
コンピュータに考え方や動きを伝えるための特別な記号です。
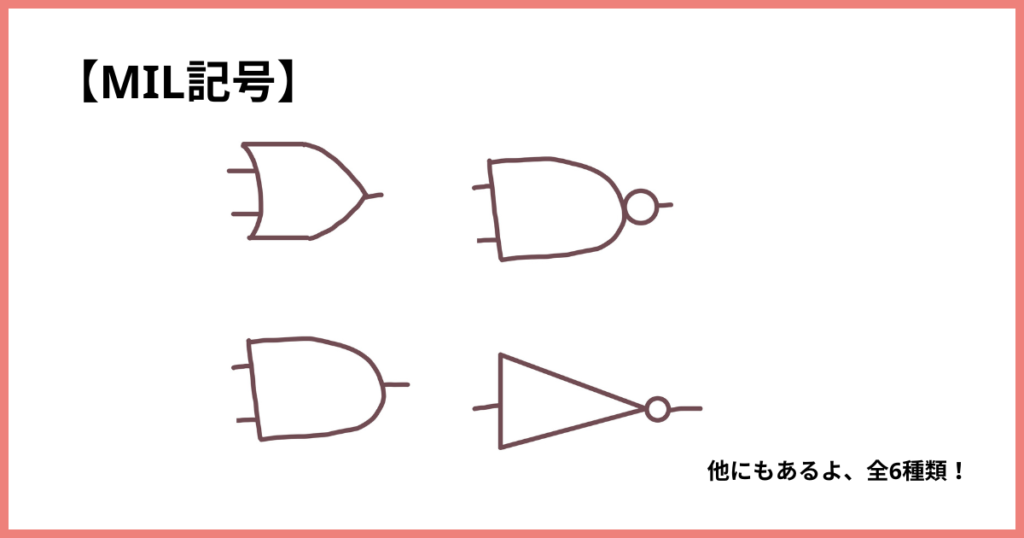
コンピュータにとっての地図記号みたいなものだよ!
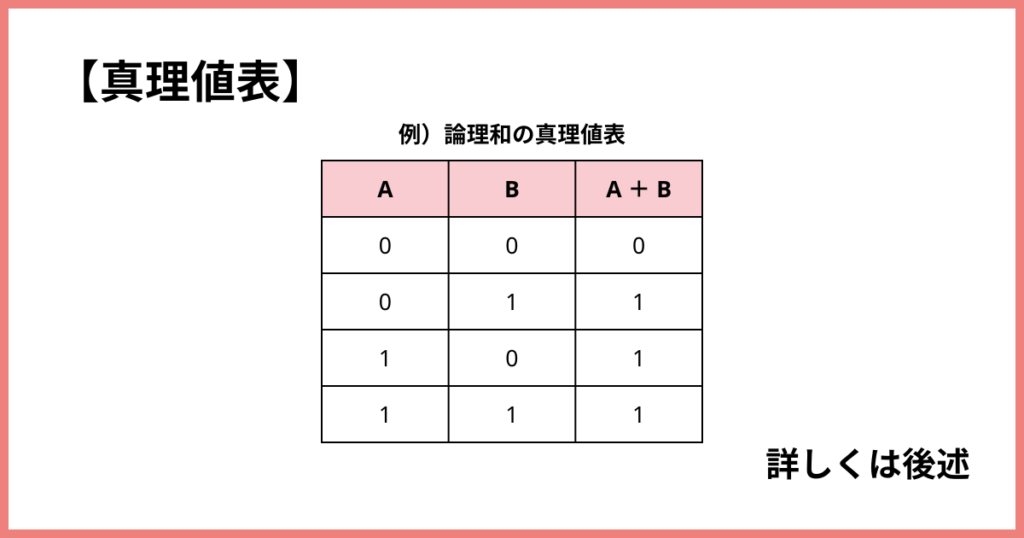
真理値表
真理値とは、「あることが本当かウソかを表す値」のこと。
例)
質問:「リンゴは赤い?」
答え:はい!
ここでは「はい(true)」が真理値だよ
つまり、
「はい(true)」か「いいえ(false)」の
どちらかで答えられるとき、
その答えを真理値と言います。
それを表にしたのが真理値表です。
ベン図
ものごとのグループ(集まり)を丸い図で表して、
それぞれの関係や共通点を分かりやすくする方法です。
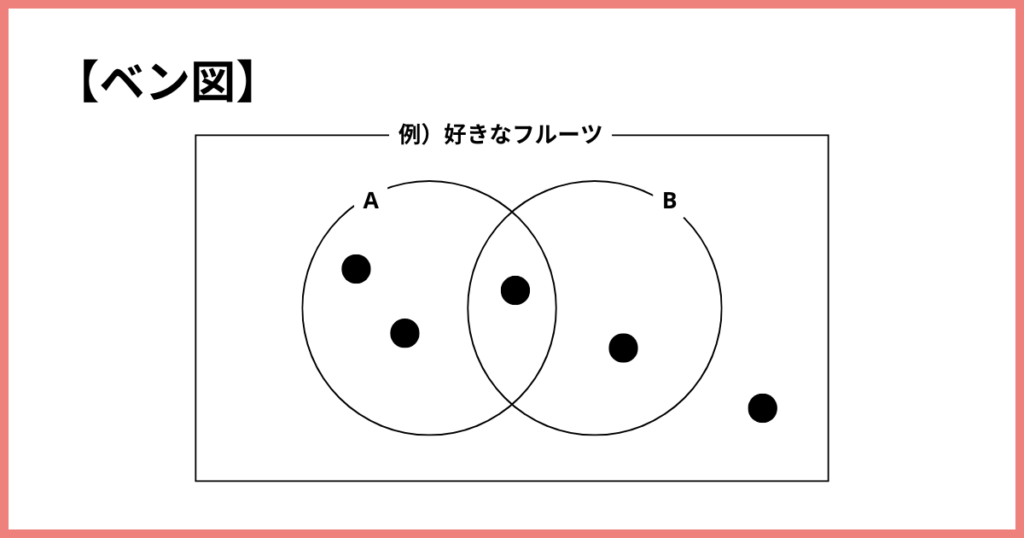
例として、好きなフルーツのベン図を作りました。
円A:「リンゴ好き」
円B:「バナナ好き」
重なり部分:「リンゴもバナナも好き」
どちらの円にも入らない部分:「リンゴもバナナも好きじゃない人」
という意味になります。
論理演算とは
論理演算とは、ものごとを
「はい(true)」か「いいえ(false)」で考えて、
決まりにしたがって答えを出す方法のことです。
試験を考えると、
「論理演算」で考えるよりは
それぞれの論理式を理解したほうがいいです。
なんとなく
「そういうものか」
と思っていただけたらマルです。
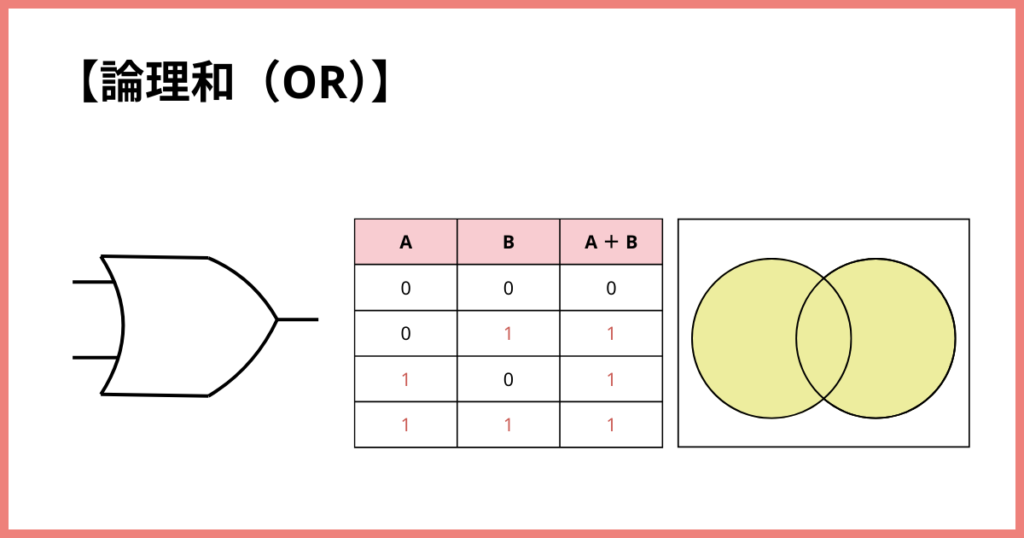
論理和(OR)
「どちらかがOKならOK!」というルールです。
質問:「今日はアイスクリームを食べた OR ケーキを食べた?」
アイスクリームを食べた → はい(true)
ケーキを食べなかった → いいえ(false)
どちらか1つでも『はい』だから、答えは『はい(true)』!
真理値でいうと、
A,Bの少なくとも一方が1であれば、
出力(A+B)は1となります。
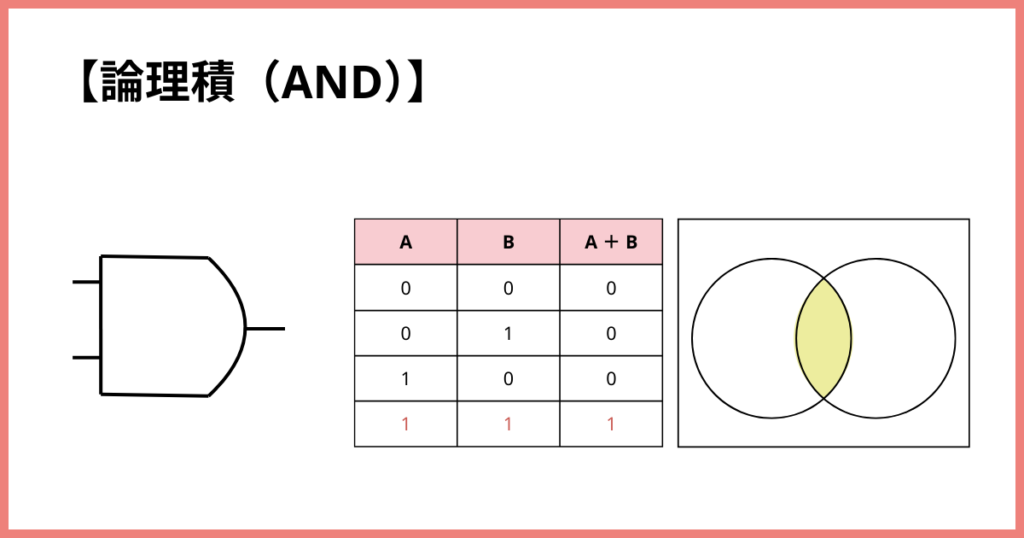
論理積(AND)
2つの条件がどちらも『はい(true)』のときだけ
『はい』になるという考え方です。
質問:「アイスクリームを食べた XOR ケーキを食べた?」
アイスクリームを食べた → はい(true)
ケーキを食べなかった → いいえ(false)
→ どちらかだけだから答えは『はい(true)』!
両方食べた → いいえ(false)!
+を◯で囲んだ記号を使うよ!
否定的論理和(NOR)
「どちらも『いいえ(false)』のときだけ『はい(true)』になる」ルールです。
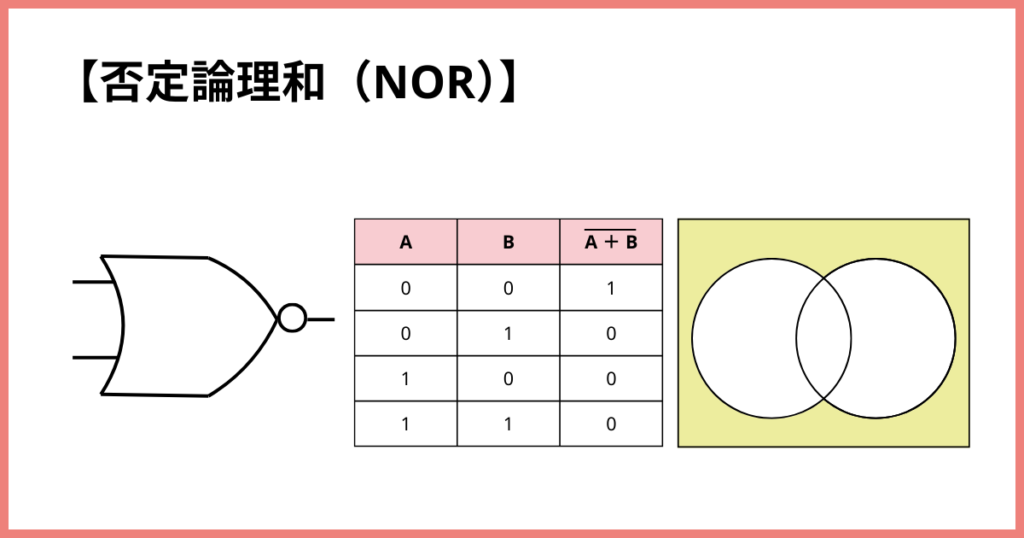
論理和と否定の組み合わせ演算です。
論理和回路の逆!
否定論理積(NAND)
「両方とも『はい(true)』のときだけ『いいえ(false)』になる」ルールです。
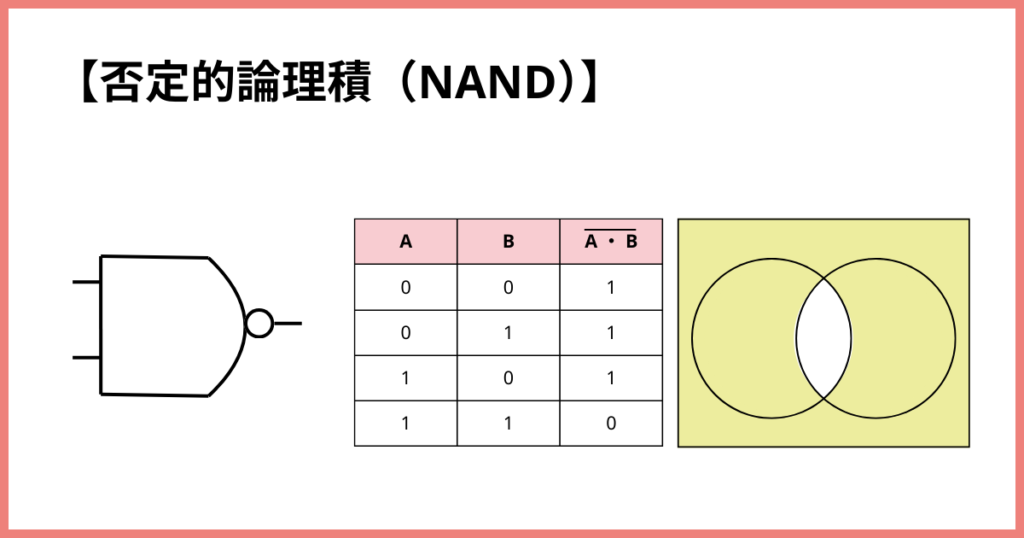
両方とも『はい(true)』 → 答えは『いいえ(false)』
どちらかが『いいえ(false)』 → 答えは『はい(true)』
論理積と否定を組み合わせた演算です。
論理積回路の逆!
まとめ:論理演算を完全解説
| 論理演算 | 意味 | 結果 | 記号 |
| 論理和 | どちらかが「はい」なら「はい」 | A = true または B = true のとき | A OR B |
| 論理積 | 両方が「はい」のときだけ「はい」 | A = true かつ B = true のとき | A AND B |
| 否定 | 今の答えをひっくり返す | A = true → A = false | NOT A |
| 排他的 論理和 |
片方だけが「はい」なら「はい」 両方は「いいえ」 |
A = true または B = true だが 両方同時ではない |
A XOR B |
| 否定 論理和 |
両方とも「いいえ」のときだけ「はい」 | A = false かつ B = false のとき | A NOR B |
| 否定 論理積 |
両方とも「はい」のときだけ「いいえ」 | 両方が『はい』なら『いいえ』 | A NAND B |
以上、お役に立てると嬉しいです♪
併せて見てね◎
続きを見る

参考【アドレス指定方式の覚え方】基本情報技術者試験に合格するまでvol.1
質問:「課題をやった AND バイトに行った?」
両方やったから答えは『はい(true)』!
課題をやった → はい(true)
バイトもした → はい(true)
否定(NOT)
「今の答えをひっくり返す」操作のことです。
簡単に言うと、
「はい(true)」を「いいえ(false)」に、
「いいえ(false)」を「はい(true)」に変えます。
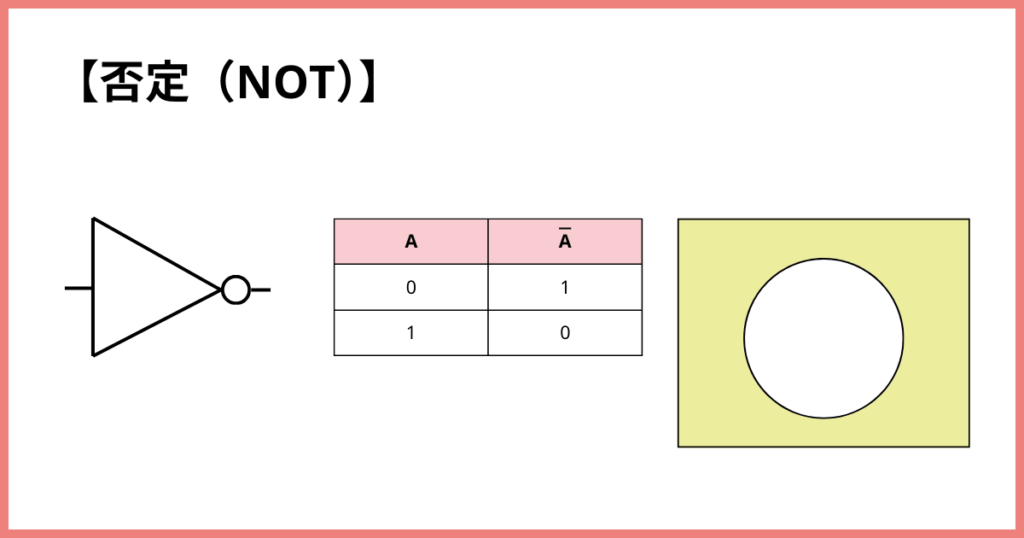
Aの上の線は否定を表すよ!
排他的論理和(EOR / XOR)
「どちらかだけがOKならOK!
でも、両方OK / 両方NGはダメ!」
というルールです。
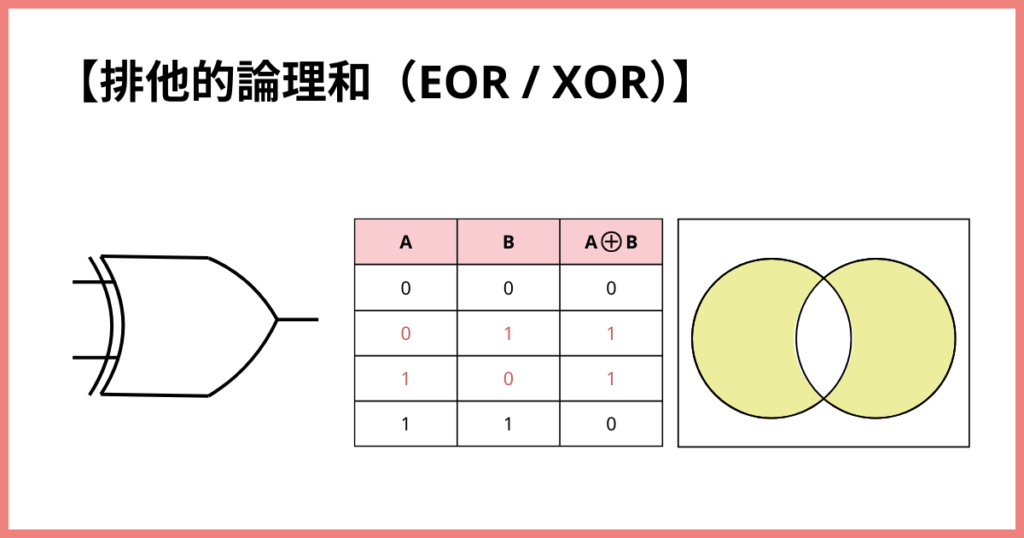
質問:「アイスクリームを食べた XOR ケーキを食べた?」
アイスクリームを食べた → はい(true)
ケーキを食べなかった → いいえ(false)
→ どちらかだけだから答えは『はい(true)』!
両方食べた → いいえ(false)!
+を◯で囲んだ記号を使うよ!
否定的論理和(NOR)
「どちらも『いいえ(false)』のときだけ『はい(true)』になる」ルールです。

論理和と否定の組み合わせ演算です。
論理和回路の逆!
否定論理積(NAND)
「両方とも『はい(true)』のときだけ『いいえ(false)』になる」ルールです。

両方とも『はい(true)』 → 答えは『いいえ(false)』
どちらかが『いいえ(false)』 → 答えは『はい(true)』
論理積と否定を組み合わせた演算です。
論理積回路の逆!
まとめ:論理演算を完全解説
| 論理演算 | 意味 | 結果 | 記号 |
| 論理和 | どちらかが「はい」なら「はい」 | A = true または B = true のとき | A OR B |
| 論理積 | 両方が「はい」のときだけ「はい」 | A = true かつ B = true のとき | A AND B |
| 否定 | 今の答えをひっくり返す | A = true → A = false | NOT A |
| 排他的 論理和 |
片方だけが「はい」なら「はい」 両方は「いいえ」 |
A = true または B = true だが 両方同時ではない |
A XOR B |
| 否定 論理和 |
両方とも「いいえ」のときだけ「はい」 | A = false かつ B = false のとき | A NOR B |
| 否定 論理積 |
両方とも「はい」のときだけ「いいえ」 | 両方が『はい』なら『いいえ』 | A NAND B |
以上、お役に立てると嬉しいです♪
併せて見てね◎
