IT未経験の私が
基本情報技術者試験の勉強をしていて、
つまずいたところや疑問に思った点を
アウトプットするシリーズです。
同じく基本情報技術者試験の勉強をしている方の参考になったら嬉しいです♪
試験合格を目指した覚え方・考え方かつ未経験独学なので、
実務的な理解方法とは異なる場合があります。
Contents
今回のテーマ:基数変換(2進数/8進数/10進数/16進数)
今回は、基数変換について理解していきます。
範囲情報
・科目A:テクノロジ系
・基礎理論
基本中の基本の超重要箇所!
今回の用語
基数
「基数(きすう)」というのは、数えるときに使う数字のことです。
たとえば、
- 1個
- 2個
- 3個
このように、「ものの数」を数えるときに使うのが基数です。
例
アイスクリームを買ったと想像してみよう!
もし友だちに「アイスクリーム何個買ったの?」と聞かれたら、
「2個だよ!」とか「3個だよ!」と答えますよね。
この「2」や「3」が基数です。
1、2、3、4、5…のような
「数を表す言葉」だと思えばいいね!
進数
「進数(しんすう)」というのは、
数を数えるときの「ルール」や「仕組み」のことです。
普段 私たちが使っている数の仕組みは10進数ですよね。
これは、「0から9までの数字」を使って数を表す方法です。
2進数
コンピュータが使う仕組みで、
「0」と「1」だけを使って数を表す方法です。
例
2進数の「10」は、10進数だと「2」を意味します。
2進数の「11」は、10進数だと「3」になるよ。
詳細はのちほど!
今は「ふ〜ん」でOKです!
16進数
こちらもコンピュータの世界でよく使われる進数です。
「0」から「9」までの数字に加えて、
「A」から「F」までを使います。
(A = 10, B = 11, … F = 15)
16進数の「1A」は、10進数だと「26」になるよ!
基数変換とは
ある進数で表された数を別の進数に変えることです。
ちょっとした「数の翻訳」みたいな感じです!
変換の例
10進数 → 2進数
2進数 → 16進数
基数変換のやり方
ここまでで基数や変換について理解できたでしょうか??
ここからは基数変換のやり方についてまとめていきます。
10進数から他の進数に変える方法
10進数を他の進数に変えるときは、
「その進数で割り続ける方法」を使います。
ポイント:余りを順番に出して、それを逆に読む!
例:10進数の25を2進数に変える場合
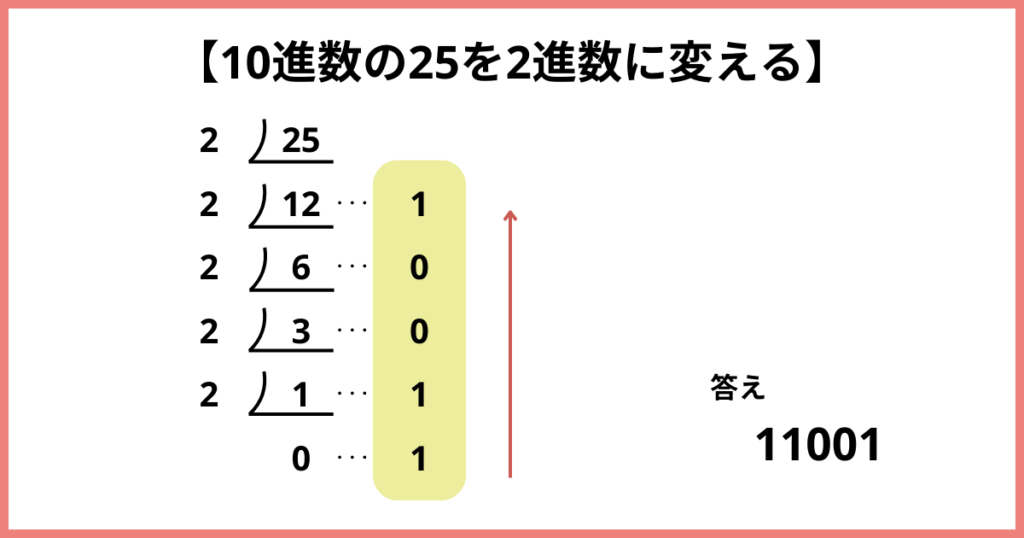
- 割り算をする
25を2で割ります- 25 ÷ 2 = 12 あまり 1
(余り「1」をメモします)
- 25 ÷ 2 = 12 あまり 1
- さらに割り算を続ける
12を2で割ります- 12 ÷ 2 = 6 あまり 0
(余り「0」をメモします)
- 12 ÷ 2 = 6 あまり 0
- 繰り返す
6を2で割ります- 6 ÷ 2 = 3 あまり 0
(余り「0」をメモします)
- 6 ÷ 2 = 3 あまり 0
- 続ける
3を2で割ります- 3 ÷ 2 = 1 あまり 1
(余り「1」をメモします)
- 3 ÷ 2 = 1 あまり 1
- 最後の割り算
1を2で割ります- 1 ÷ 2 = 0 あまり 1
(余り「1」をメモします)
- 1 ÷ 2 = 0 あまり 1
- 余りを逆に読む
余りを下から上に読むと、「11001」
11001が、10進数「25」を
2進数に変換した結果です!
他の進数(例:16進数)の場合
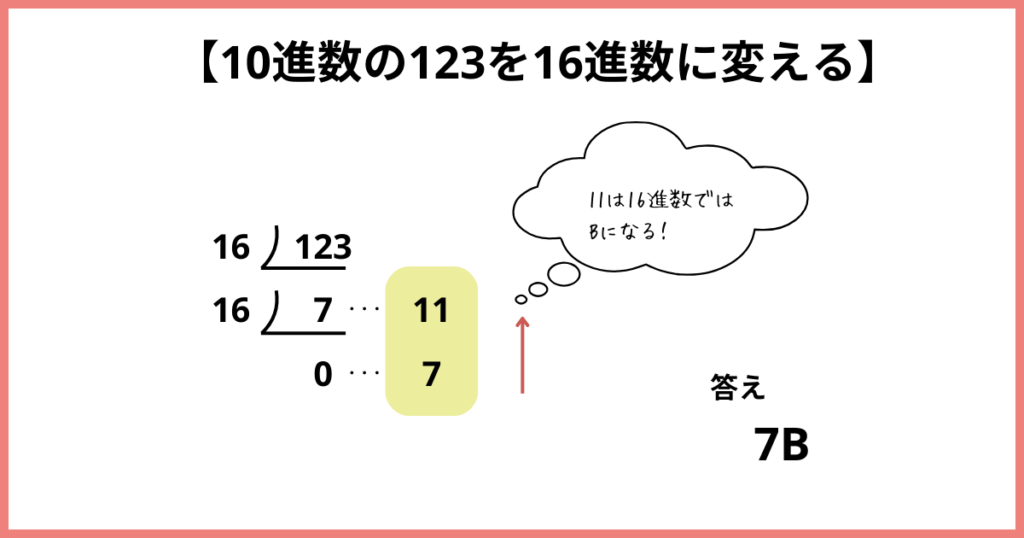
2進数以外でも同じ方法で変換ができます。
たとえば、10進数「123」を16進数に変えるなら:
- 123 ÷ 16 = 7 あまり 11 → 余りの11は16進数では「B」。
- 7 ÷ 16 = 0 あまり 7。
よって、答えは「7B」です。
他の進数 → 10進数への変換
他の進数を10進数に変えるときは、
「各桁を計算して足す」方法を使います。
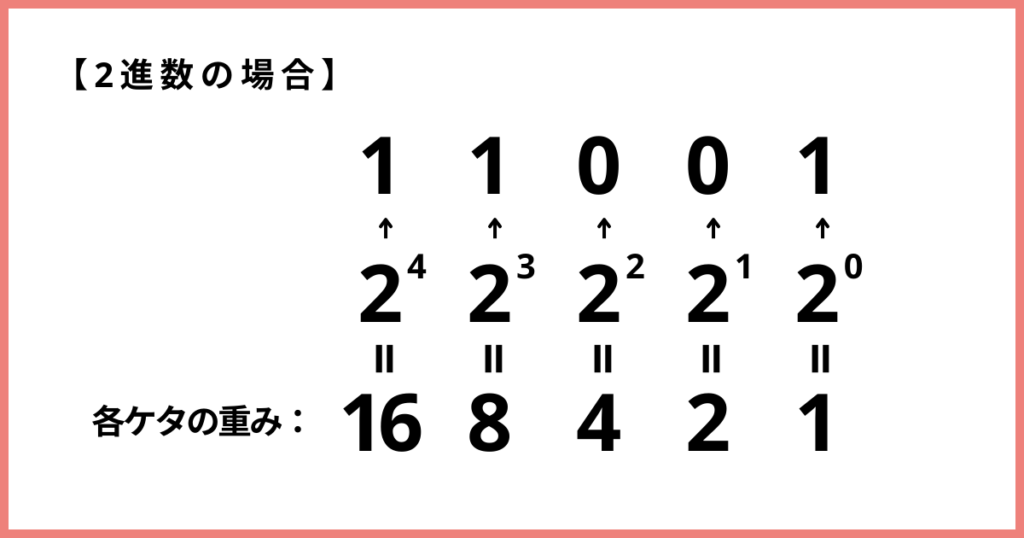
ポイント:桁ごとに「その進数の重み」をかけて足していく!
例:2進数「11001」を10進数に変える場合
- 桁ごとの重みを考える
2進数では、右から順に桁の重みは次のようになります:- 1番右(1の位)→ 2^0 = 1
- 次(10の位)→ 2^1 = 2
- 次(100の位)→ 2^2 = 4
- 次(1000の位)→ 2^3 = 8
- 1番左(10000の位)→ 2^4 = 16
- 各桁の計算をする
2進数「11001」の各桁を見て、それぞれ計算します:- 1番左の1 → 1 × 16 = 16
- 次の1 → 1 × 8 = 8
- 次の0 → 0 × 4 = 0
- 次の0 → 0 × 2 = 0
- 1番右の1 → 1 × 1 = 1
- 足し算をする
16 + 8 + 0 + 0 + 1
= 25
答えは「25」
^0や^1は、0乗、1乗ってこと!
どんな数字でも0乗は1になるよ!
他の進数(例:16進数)の場合
たとえば、16進数「1A」を10進数にするなら:
- 桁ごとの重みを考える(16進数では、桁の重みは16の累乗):
- A(=10) → 10 × 16^0 = 10
- 1 → 1 × 16^1 = 16
- 足し算をする:
- 16 + 10 = 26
答えは「26」です。
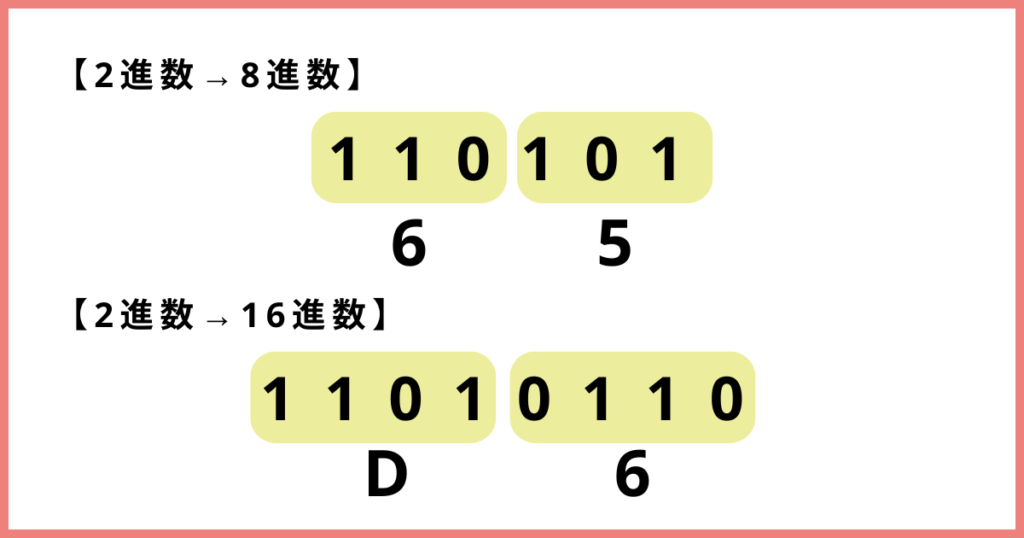
2進数から8進数への変換
8進数は、2進数の3桁を1グループにして変換します。
例:2進数「110101」を8進数に変換
- 右から3桁ずつ区切る
- 2進数「110101」を右から3桁ずつ区切ります:
- 「110」と「101」
※ もし3桁に足りない場合は、
左側に「0」を足して3桁にします。
- 各グループを8進数に変換
- 2進数「110」 = 1 × 2^2 + 1 × 2^1 + 0 × 2^0 = 4 + 2 + 0 = 6
- 2進数「101」 = 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 4 + 0 + 1 = 5
- 結果を並べる
- 8進数では「65」になります。
2進数から16進数への変換
16進数は、2進数の4桁を1グループにして変換します。
例:2進数「11010110」→ 16進数
- 右から4桁ずつ区切る
- 2進数「11010110」を右から4桁ずつ区切ります:
「1101」と「0110」
※ もし3桁に足りない場合は、
左側に「0」を足して4桁にします。
- 2進数「11010110」を右から4桁ずつ区切ります:
- 各グループを16進数に変換
- 2進数「1101」 = 1 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 8 + 4 + 0 + 1 = 13
※ 16進数では13は「D」。 - 2進数「0110」 = 0 × 2^3 + 1 × 2^2 + 1 × 2^1 + 0 × 2^0 = 4 + 2 = 6
- 2進数「1101」 = 1 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 8 + 4 + 0 + 1 = 13
- 結果を並べる
- 16進数では「D6」になります。
まとめ
10進数 → 他の進数
- 割り算を繰り返して、余りを出す。
- 最後に余りを逆に読む。
他の進数 → 10進数
- 各桁の値に「進数の重み」を掛け算する。
- 全部足し算して答えを出す。
2進数 → 8進数
- 右から3桁ずつ区切る(足りない場合は左に「0」を足す)。
- 各グループを計算し、8進数に変換する。
2進数 → 16進数
- 右から4桁ずつ区切る(足りない場合は左に「0」を足す)。
- 各グループを計算し、16進数に変換する。
慣れると簡単にできるので、
たくさん問題を解いてみてください!
以上、お役に立てると嬉しいです♪
